核心思想
根据队列排队延时进行端口选择,从而解决packet spraying的乱序问题。
Motivation
这篇论文是对paclet-level load balancing的工作的重要改进,解决其最明显的乱序问题。亮点:在motivation部分通过实验对已有packet-level,flow-level,flowlet-level的缺点进行了直观展示。
-
Out-of-order problems in RPS
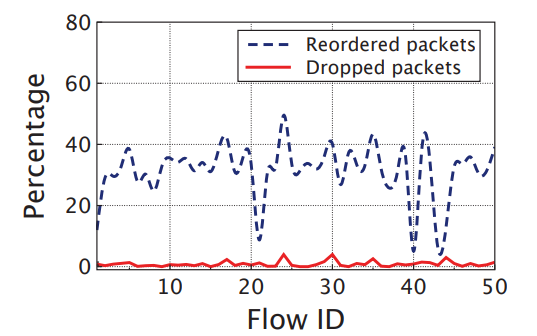
50 flows (from 50KB to 200KB) in heavy-tailed distribution. The percent of reordered packets is about 30% on average, while the packet loss rate is almost zero. The reason is that, even when the traffic load is not high, RPS randomly spreads the packets of each flow to all paths, unavoidably resulting in out-of-order problem.
-
Low link utilization in ECMP and LetFlow
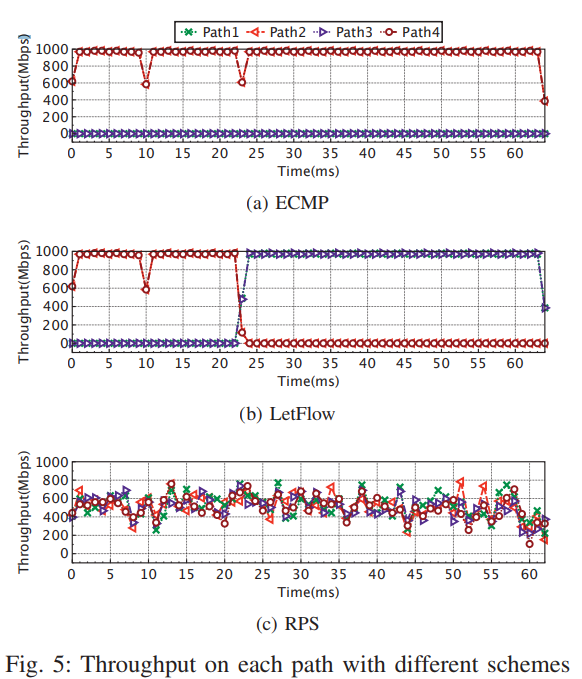
只有RPS能实现所有链路的最高链路利用率(如果没有乱序问题)。
Design
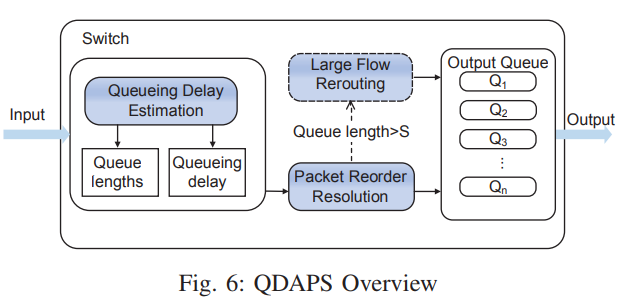
核心算法有两个, 一个是同一个流的包根据queue delay选择端口避免乱序, 一个是对于大流reroute
-
Packet Reorder Resolution
思路比较直观:每个流的第一个包,选择队列长度最小的端口;后面到达的包,选择端口的时候确保排队时延要比它的上一个包的剩余排队时延要大。
When a packet $p_{i}$ in flow $f$ arrives at time $t_{i}$, the queueing delay $QD_{i}$ is calculated as
\[QD_{i} = \frac{M \times (l_{i} + 1)}{C}\]where $M$ is the packet size, $l_{i}$ is the queue length of $p_{i}$’s destined output port, and $C$ is the link bandwidth corresponding to the output port.
When the following packet $p_{i+1}$ in flow $f$ arrival at time $t_{i+1}$, the remaining queueing delay $RQD_{i}$ of $p_{i}$ is
\[RQD_{i} = QD_{i} + t_{i} − t_{i+1}\]Then chooses $d$ output ports with larger queueing delay than $RQD_{i}$, finds the one with the current minimum queue length between these $d$ ports.
-
Large Flow Rerouting
按照上述思路解决乱序的问题后,对于大流会带来一个问题:大流在buffer中包数目多,为保证新的包的queue delay比它上一个包剩余delay大,可能就只能排在上一个包后面,到了最后大流的所有包都挤在了一个(某几个)端口。因此论文当发现队列长度超过阈值$S$时,对流进行reroute。但是要在中间找一个
tradeoff:降低reroute对乱序和rate reduction的影响。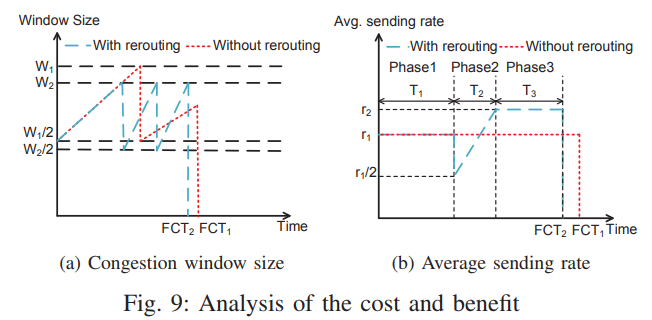
论文针对DCTCP进行了分析。对于DCTCP,队列长度维持在 $K$,则最大拥塞窗口为:
\[W_{1} = C \times RTT + K\]When the congestion window grows from $\frac{W_{1}}{2}$ to $W_{1}$, it takes $\frac{W_{1}}{2}$ RTTs. During each round, the average congestion window and queueing delay are $\frac{3W_{1}}{4}$ and $\frac{K}{C}$ , respectively. Then we get the average sending rate $r_{1}$ as:
\[r_{1} = \frac{\frac{3W_{1}}{4}}{RTT+ \frac{K}{C}}\]
\[FCT_{1} = \frac{Y}{r_{1}} = \frac{4Y \times (RTT+ \frac{K}{C})}{3W_{1}}\]如果不进行reroute,则流完成时间$FCT_{1}$为:$Y$是 流大小(单位为包)。
\[W_{2} = C \times RTT + S\]如果当队列长度超过S就进行reroute, 最大拥塞窗口$W_{2}$为:计算 $FCT_{2}$: 需要考虑三个阶段.
(1) 队列长度小于$S$,拥塞窗口从1增加到$W_{2}$。需要$W_{2}$个RTT,平均窗口为$\frac{W_{2}}{2}$。
在这一阶段发送的流大小$S_{1}$为:
\[S_{1} = \frac{W_{2}}{2} \times W_{2}\]这一阶段时间$T_{1}$为:
\[T_{1} = \frac{S_{1}}{r_{1}}\](2) 平均速率从$r_{1}$降为$\frac{r_{1}}{2}$,再升至$r_{2}$。平均排队延时为$\frac{S}{2C}$。
则$r_{2}$:
\[r_{2} = \frac{\frac{3W_{2}}{4}}{RTT+ \frac{S}{2C}}\]拥塞窗口从$\frac{W_{2}}{2}$升为$W_{2}$。在这一阶段发送的流大小$S_{2}$为:
\[S_{2} = (W_{2} - \frac{W_{2}}{2}) \times \frac{W_{2} + \frac{W_{2}}{2}}{2}\]平均发送速率:$\frac{\frac{r_{1}}{2} + r_{2}}{2}$. 这一阶段时间$T_{2}$为:
\[T_{2} = \frac{S_{2}}{\frac{\frac{r_{1}}{2} + r_{2}}{2}}\](3) 剩余的流按照速率$r_{2}$发送。
这一阶段时间$T_{3}$为:
\[T_{3} = \frac{Y-S_{1}-S_{2}}{r_{2}}\] \[FCT_{2} = T_{1} + T_{2} +T_{3}\]要降低流完成时间,就要保证$FCT_{1} \geq FCT_{2}$,可得到$S$:
\[S \approx \sqrt{\frac{12YC-8Yr_{1}}{6C-3r_{1}}} - C \times RTT\] -
QDAPS* :根据Leaf-to-leaf Delay 信息选端口
QDAPS是个switch-local的方案。The local congestion state on the leaf switch is not always consistent with the global or leaf-to-leaf information about congestion.
具体做法:源leaf发送数据包时打时间戳,目的leaf收到数据包时将到达时间减去发送时间获得Leaf-to-leaf Delay,通过反方向的数据包或者ACK包捎带回去(类似CONGA)。源leaf交换机收到后,将Leaf-to-leaf Delay + local queueing delay作为选端口标准。
Implementation and evaluation
实验充分。
-
Simulations. ns-2
虽然一些实验规模很小,30条流等。但是也能说明问题。
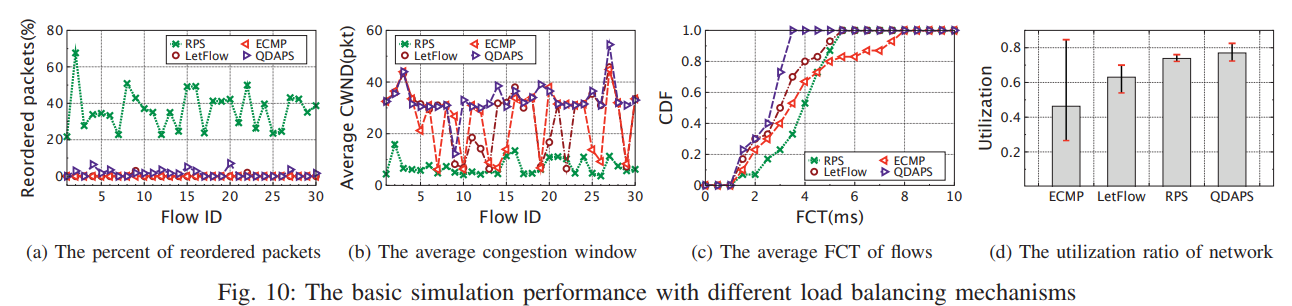
-
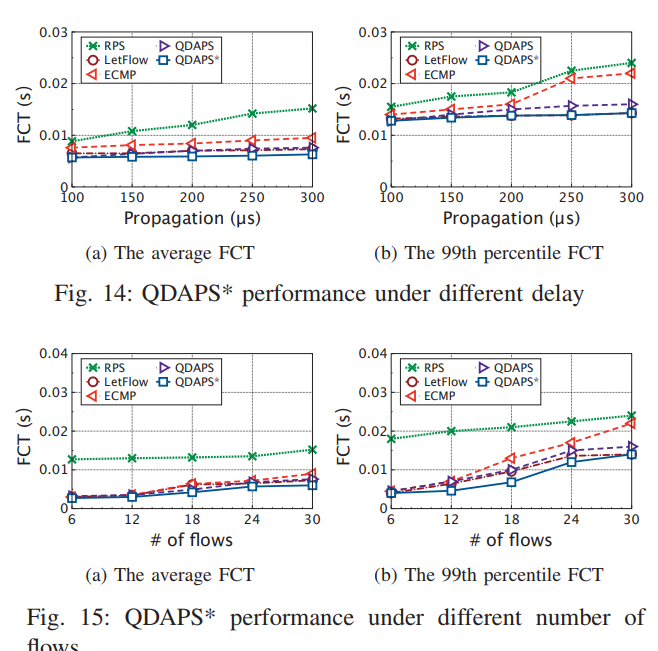
Testbed. Mininet 交换机实现用的P4(16). 20Mbps 规模较小. 不同流数目 不同传播时延 不同链路带宽
My thinking
参考文献
QDAPS: Queueing Delay Aware Packet Spraying for Load Balancing in Data Center